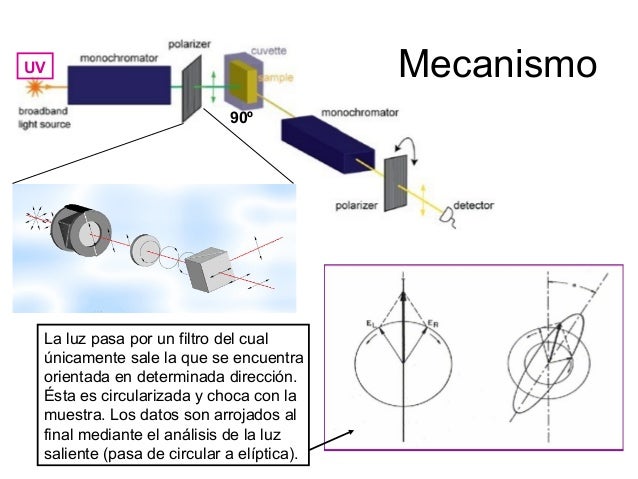
Muchas veces queremos obtener las mejores condiciones para realizar nuestro experimento, las cantidades precisas, proporciones exactas o valores óptimos de cualquier cosa que se os ocurra. Muchas veces con un par de ensayo del factor más importante es suficiente y conocemos el valor deseado pero... ¿Y si tenemos muchos factores? ¿Y si la variación de la respuesta depende de la proporción de varios factores a la vez? ¿Y si los valores óptimos de varias respuestas no coinciden? ¿Y si quiero obtener una superficie de respuesta para saber dentro de que intervalos me puedo mover al realizar mis experimentos?
No te preocupes, hoy voy a intentar ayudarte con todo esto ayudándome de las matemáticas y la estadística, utilizando algunos ejemplos de mi propia tesis doctoral. Vamos...
¿Qué es la Quimiometría?
Según la IUPAC en su Gold Book, la quimiometría es la aplicación de la estadística para el análisis de datos químicos (de química orgánica, analítica o médica), el diseño de experimentos químicos y de simulaciones. Hoy me voy a centrar en el diseño de experimentos y cómo hacerlo con el mínimo número de experimentos.
La metodología más empleada es la basada en diseños factoriales aunque hay otras metodologías como el simplex que, en algunos casos, pueden obtener resultados similares con un menor número de experimentos. La desventaja del simplex frente a los diseños es que no se conoce la influencia de cada una de las variables, sus interacciones ni el número total de experimentos a realizar a priori.
El objetivo de un diseño factorial es estudiar el efecto de varios factores sobre una o varias respuestas, cuando se tiene el mismo interés sobre todos los factores. Por ejemplo, uno de los objetivos particulares más importantes que en ocasiones tiene un diseño factorial es determinar una combinación de niveles de los factores en la que el desempeño del proceso sea mejor.
Los factores pueden ser de tipo cualitativo (máquinas, tipos de material, operador, la presencia o ausencia de una operación previa, etc.), o de tipo cuantitativo (temperatura, humedad, velocidad, presión, etc.). Para estudiar la manera en que influye cada factor sobre la variable de respuesta es necesario elegir al menos dos niveles de prueba para cada uno de ellos. Con el diseño factorial completo se ensayar aleatoriamente todas las posibles combinaciones que pueden formarse con los niveles de los factores a investigar.
Los diseños factoriales se denominan de acuerdo al número de ensayos que se realizan en cada variable. Si suponemos un diseño de dos variables, una con dos y otra con tres ensayos de cada variable o niveles, tendríamos un cuadrado con dos puntos (en los extremos) en dos de los lados y los otros dos con tres, resultando un total de 2×3=6 puntos del diseño factorial. Habitualmente, se suele emplear el mismo número de experimentos en todas las variables, resultando diseños del tipo 3×3 o 2×2×2, resultando diseños tipo 32 o 23, o nv, donde n es el número de niveles y v el número de variables.
De igual manera, es habitual normalizar los valores de las variables aunque en la mayoría de los casos no es necesario. Para normalizar, se le otorga al punto menor el valor de -1 mientras que al mayor se le asigna 1. El resto de los puntos se asignan proporcionalmente a esta diferencia. Por ejemplo, si hay un punto central, este punto tendrá el valor de 0.
Una vez tenemos esto, en teoría podríamos preparar diseños factoriales con muchas variables y muchos puntos por variable, estamos únicamente limitados por nuestra capacidad de realizar tantos experimentos, ya que crecen exponencialmente. Muchas veces los experimentos resultantes son demasiados para realizarlos en una única jornada de trabajo o, incluso, en dos. Para evitar estos trastornos existen los diseños factoriales fraccionados, en los que únicamente se ensaya una fracción de los puntos, resultando una reducción muy importante de ensayos (en un factor de 1/2p). Estos diseños se expresan como nv-p, siendo p la fracción de puntos no ensayados que acabo de comentar. Por ejemplo, en un diseño 23-1 únicamente se ensayan (2×2×2)/2= 4 puntos de los 8 originales de los que cuenta el diseño. Además de una reducción de los experimentos muy importante también hay información que se pierde por el camino, en este caso, hay interacciones que se vuelven indistinguibles. Vamos a verlo con un ejemplo concreto de mi tesis doctoral.
Para optimizar una separación quiral de tres profenos ensayé cuatro variables (pH, porcentaje de 2-propanol (2-PrOH) y concentración de sales de la disolución reguladora de pH (Tampón) y de trietilamina (TEA), un modificador para el reconocimiento quiral) para determinar cuáles eran las más influyentes en mi respuesta, resultando 24=16 fases móviles a ensayar en un día, cosa bastante complicado, por lo que decidí usar un diseño factorial fraccionado. Para evaluar los resultados utilicé 7 respuestas. La matriz de datos obtenida fue la siguiente:
 |
| Matriz de diseño factorial fraccionado |
En la parte inferior de la tabla se pueden ver los extremos de cada variable del diseño. Una vez con los resultados, vamos a proceder a evaluarlos. Existen diferentes maneras de evaluarlos, por ejemplo mediante análisis de la varianza (ANOVA), pero una de las maneras más intuitivas de interpretar estos diseños es mediante diagramas de Pareto, en los que se se indica mediante barras la influencia y el signo de la interacción de cada una de las variables. Además, en los diagramas de Pareto estandarizados, se puede saber qué variables son estadísticamente significativas. Para estimar los errores estadísticos hay que hacer repeticiones en algún punto del diseño, en este caso en el centro del diseño. Veamos el diagrama de Pareto estandarizado para el factor de retención del R-ketoprofeno (R-KPF):
 |
| Diagrama de Pareto estandarizado |
Se observa que, de todos los factores estudiados, únicamente el pH y el porcentaje de 2-PrOH son significativos al sobrepasar la línea vertical que muestra la variabilidad estadística. Las otras dos variables (Tampón y TEA) así como las interacciones entre las variables no son significativas. Además indica que ambas variables significativas tienen influencia negativa sobre la respuesta, es decir, que al aumentar el pH o el porcentaje de 2-PrOH disminuye kR-KPF, es decir, se retiene menos.
Hay que destacar de igual manera que las únicas interacciones que aparecen son con el pH (A) ya que, al reducir el número de ensayos, hemos perdido esa información. En este caso, la interacción AB se confunde con la CD, la AC con la BD y la AD con la BC.
Una vez definidas las dos variables más importantes, procedí a optimizarlas mediante un diseño factorial completo de superficie de respuesta, es decir, utilicé un diseño factorial completo (sin fraccionar) en el que cada dimensión tenía más de dos puntos, pudiendo ajustarlos a una curva para modelizar los cambios. Para ello utilicé este diseño 32:
 |
| Matriz del diseño factorial completo |
En este diseño tampoco se obtuvo ninguna interacción significativa, siendo en la mayoría de los casos únicamente los factores principales como significativos (lo puedes comprobar en los diagramas de Pareto). A partir de estos datos, se realizó una superficie de respuesta para cada respuesta (valga la redundancia), obteniéndose 7 puntos óptimos...
¿Y ahora qué? ¿Cuál de todas es la óptima total? ¿Importan igual todas las respuestas? En este caso se llevó a cabo una optimización multi-respuesta, en la que algunas de las respuestas se obviaron o se ponderaron para dar lugar a un único valor, la deseabilidad. Es esta función la que haremos única para cada punto de la matriz, teniendo, finalmente, una solución por punto y representando la superficie de respuesta obtenida con su ecuación.
 |
| Función de deseabilidad |
En esta función de deseabilidad, el punto máximo (o mínimo) sería el valor óptimo general aunque no sea el particular de alguna respuesta. Estas superficies de respuesta pueden ser de más de dos dimensiones, resultando las mallas de respuesta, en las que hay más de dos variables y su representación es tridimensional.
 |
| Malla de respuesta para la extracción del gel Extraplús |
Todos estos resultados han sido obtenidos con el software Statgraphics Centurion XVI. Este software tiene un asistente para el diseño de experimentos que te guía a través de todos los pasos para realizar tu diseño. Lo puedes descargar y probar gratis durante 30 días aquí. Para más teoría recomiendo el libro "Análisis y diseño de experimentos" de Humberto Gutiérrez Pulido y Román de la Vara Salazar. Si no lo encontráis en la biblioteca, es posible encontrarlo en buena calidad por la red (🏝🛳, jou jou).
Hasta aquí el tema de hoy, escogido por la encuesta de Facebook. Como siempre digo, si tienes dudas, quieres comentarios más a fondo o cualquier duda puedes preguntarlo en los comentarios de abajo. También me puedes pedir la tesis completa donde está más explicado y tienes el contexto completo de estos diseños.
Nos vemos la semana que viene!
Cuídate!!






.jpg)